25 ++ 算数 速さ 問題 追いつく 528595-算数 速さ 問題 追いつく

 驚くばかり 小6 算数 速さ 追いつく 数学 中1 45 方程式9 1次方程式の利用 速さ 追いつく 文章問題 小6 算数 速さ 解説 動画 Youtube 旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun 旅人算 の問題の解き方 小学生に教えるための分かり 方程式（速さ）追いつく問題解き方 問題 兄が家を出発してから12分後に弟が家を出発して、兄を追いかけました。 兄の進む速さが分速60m、弟の進む速さが分速1mのとき、弟は家を出発してから何分後に兄に追いつくか。 それでは、上の分からなかった問題が解けました！ ありがとうございました！ すぐに計算できたので、大変便利で役に立ちました。 趣味です。 どれもこれも役

旅人算 算数の教え上手 学びの場 Com

算数 速さ 問題 追いつく

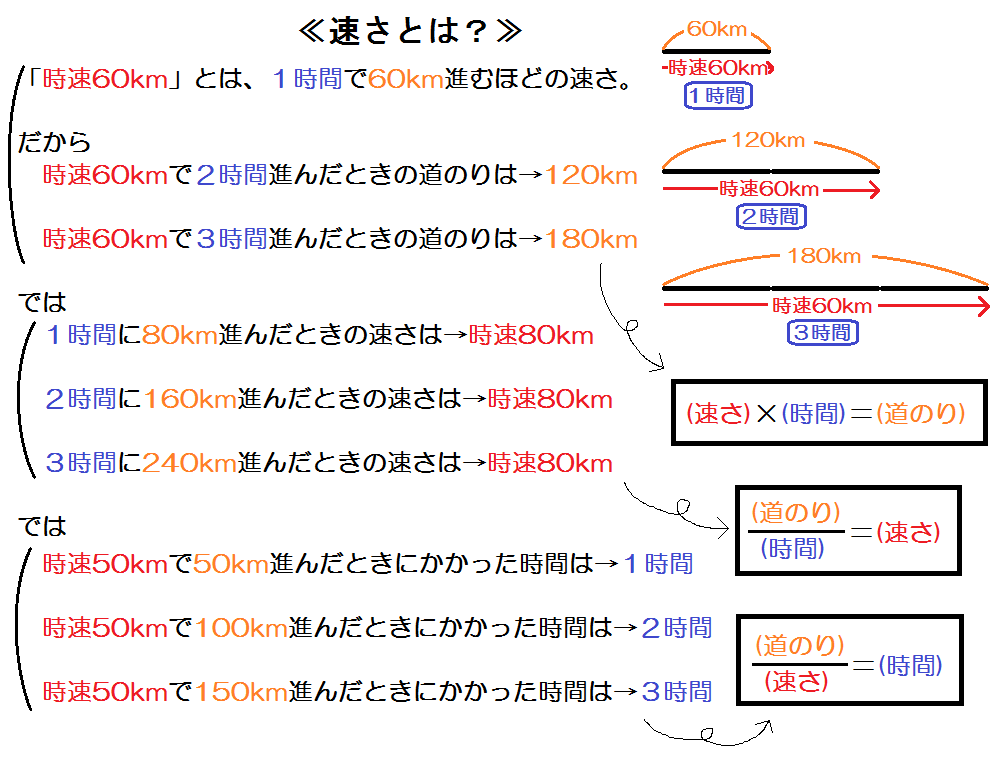
算数 速さ 問題 追いつく-Hello School 算数 通過算 練習問題 解答と解説 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。 1． 長さ0mの列車が時速54kmの速さで、1300mのトンネルに入り始めてから文章題 (速さ) 「速さが変わる」 AからBを通ってCまでの道のりが1mで、 AからBまでがxmなら、 BからCまでは (1x)mである 例題 ユウジ君の家から公園を通って駅まで行くと1000mある。 ユウジ君が家を出てから公園まで毎分80mで歩き、公園から駅までは

中学受験 算数 速さの重点ポイントまとめ 比を使った裏技公開 中学受験アンサー

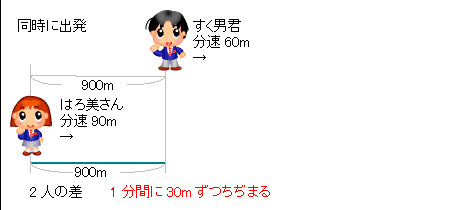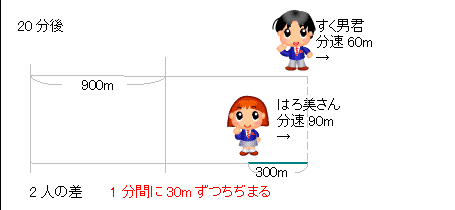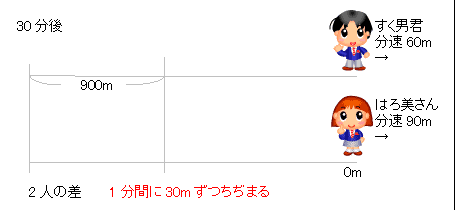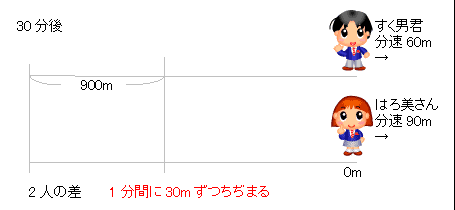
3人の速さの比を連比で解くと、 すく男君：はろ美さん：Yousuke先生＝5：9：10 はろ美さんの速さを分速9m、Yousuke先生の速さを分速10mとすると、 最初のきょりの差は9×4分＝36m。 1分間で1mずつちぢまるので、Yousuke先生がはろ美さんに追いつくのは、36分後。小学生の算数 変化と関係・データの活用（数量関係） 練習問題プリント 無料ダウンロード・印刷 小学6年生 速さ・時間・道のり 練習問題プリント お気に入り練習問題 ・ その5_速さの差を考える（2）・追いつく 答え 次の にあてはまる数を求めなさい。 (1) 弟の分速は80m、兄の分速は100mで、弟が家から240mのところを歩いている時、兄も家を出発して同じ方向に歩き出しました。

優れた 算数 速さ 問題 追いつく 6年生の速さの問題です 解説と 式を教えてくれれば 嬉しいです 6 旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun小学生の算数 変化と関係・データの活用（数量関係） 練習問題プリント 無料ダウンロード・印刷;1 周1800m の池があります。この池のまわりを太郎と次郎がそれぞれ同時に同じ場所から反対方向に歩き始めると，15 分後に2 人は出会います。また

方程式の文章題(速さ の問題) 方程式をたてて求めよ。 (1) A君はいつも毎分70mの速さで歩いて学校へ行く。今日は家を出るのがいつもより9分遅かったので 毎分100mの速さで走っていったらいつもと同じ時刻に学校に着いた。A君の家から学校までは何mか。流水算の練習問題③ 応用編 流水算の応用問題 こちらは、流水算の応用問題を載せているページです。 流水算の詳しい解説はこちら、基本問題はこちら、標準問題はこちらへどうぞ。 川を上る時は、川の流れの速さのぶん船は遅くなります。(1)このバスの速さは時速何kmですか。 (2)アは何分ですか。 (3)バスが坂下を出発してから5分後にはろ美 さんがタクシーで追いかけます。バスが坂中 を出発するまでに追いつくには、タクシーは 時速何km以上何km以下の速さで走れば よいですか。

中学数学 １次方程式 文章題の解き方 速さ 時間 道のり

何分後に追いつくでしょう 妹が分速５０メートルで家を９時に出発し 数学 教えて Goo

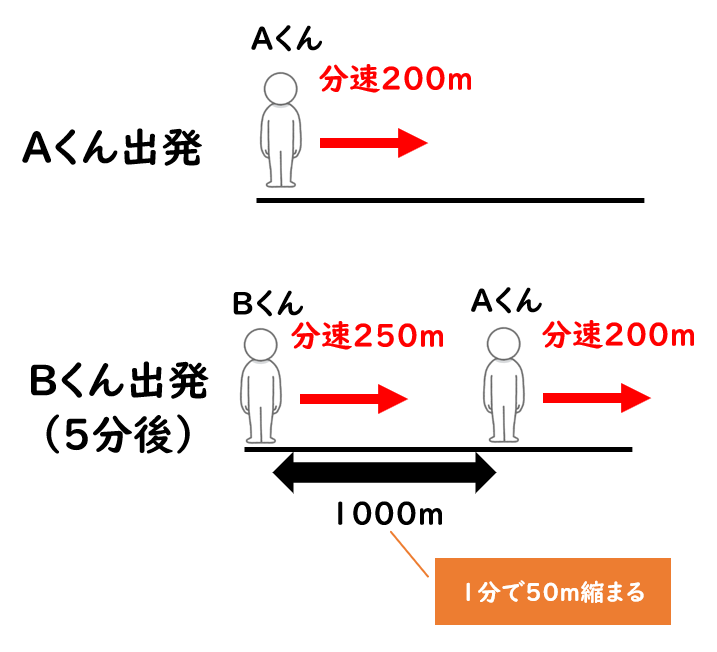
Aが出発してから30分後にBが出発するので、 Bが出発するまでにAが進む距離は、距離 ＝ 速さ × 時間より 40 × 30 ＝ 10m 追いかける場合にかかる時間は、 時間 ＝ 距離 ÷ (Bの速度 － Aの速度)より 10 ÷ (60 － 40) ＝ 60分になる。 答え：60分Hello School 算数 旅人算 練習問題 解答と解説 はろ美さんの歩く速さは分速70m、すく男君の歩く速さは分速50mです。2人が同じ場所を はろ美さんがすく男君に追いつくのは、15分後から1000÷（250－50）＝5分後この問題を見ますと、「旅人算」の学習は次のような流れになっていることがわかります。 ではC問題以降はどうでしょうか。 （D問題より） 分速100mの速さでいけば、目的地に予定の時間より1分早くつき、分速80mの速さでいけば、10分遅くつきます。

８ １０ グラフからたかしくんとバスの速さをとらえるには さんすうがく パート 2

3

途中で速さが変わる文章問題の解き方、コツを解説！ 割合を使った全校生徒の増減に関する文章題の解き方を解説！ 池の周りを追いつく速さの問題を解説！←今回の記事 鉄橋、トンネルを列車が通過する問題はこれでバッチリ！「速さ」という概念も難しいため、それを応用した旅人算も一見解けそうにないと感じられる問題が多いです。 そのため、 「算数」のカテゴリの中ではトップクラスに難易度が高い問題として知られています 。 旅人算は、就活にも利用されています。旅人算（追いつく時間） 使いやすいです。 すごく楽だった。 旅人算で分からない問題が有ったからです?

旅人算の基本 図をかいて整理しよう

Newみんなの算数講座41 ２倍じゃなくて３倍になる秘密 中学受験の算数知恵宝庫

文章題 (速さ) 「追いつく1」 注意点 表にまとめる 求めるものをxにする。 先に出た人と後から出た人の 距離は同じ 。 歩いていた (走っていた)時間は 先に出た人のほうが長い 。 例題 弟が家を出て毎分80mで歩いて行った。 兄がその5分後に毎分100m速さの練習問題 ｜ 16年06月18日18時00分 「第292回 苦手の克服 速さ3」 「苦手の克服 速さ」について考えています。 前回はその2回目として、「線分図解法の使い方」について、 (1)線分図は「事件（着く・出会う・追いつく・速さを変える）が発生」する 算数 速さ 旅人算の苦手を克服！ 速さの問題の解き方とは独立した全く別のものとしてとらえて教えてあげるほうが分かりやすいかもしれませんね。 この問題は兄と弟が同時に同じ方向に出発して兄が弟に追いつくまでの時間を求める問題です。

中学受験 旅人算とは 基本公式から往復など応用問題 ダイヤグラムまで そうちゃ式 受験算数 2号館 図形 速さ

旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun

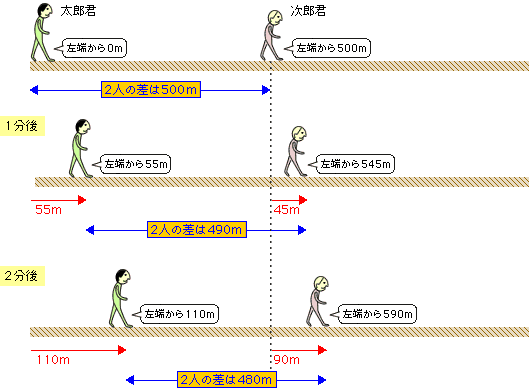
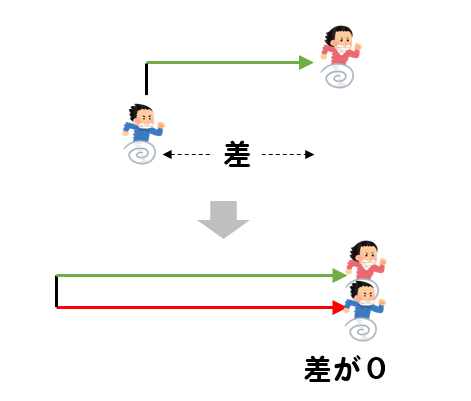
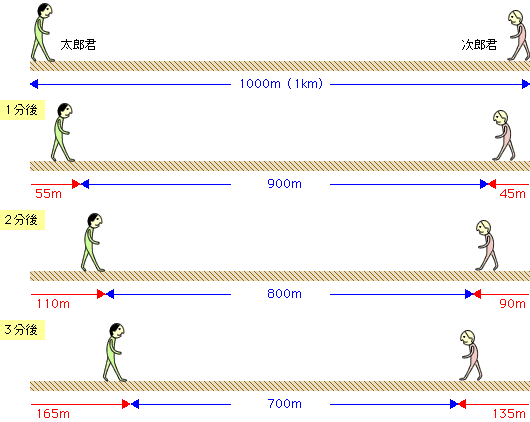
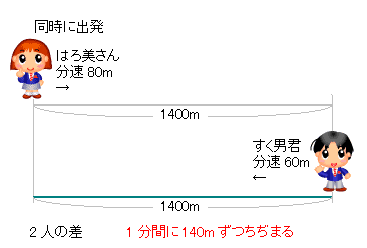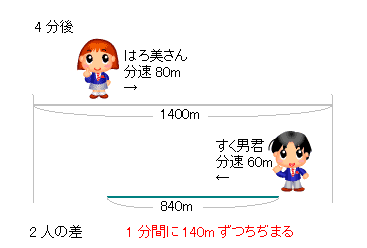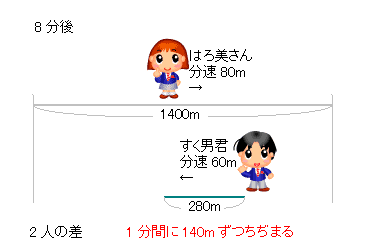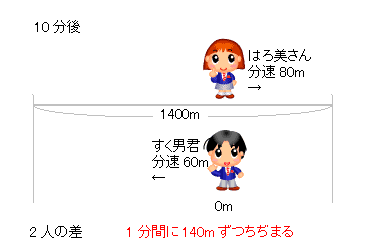
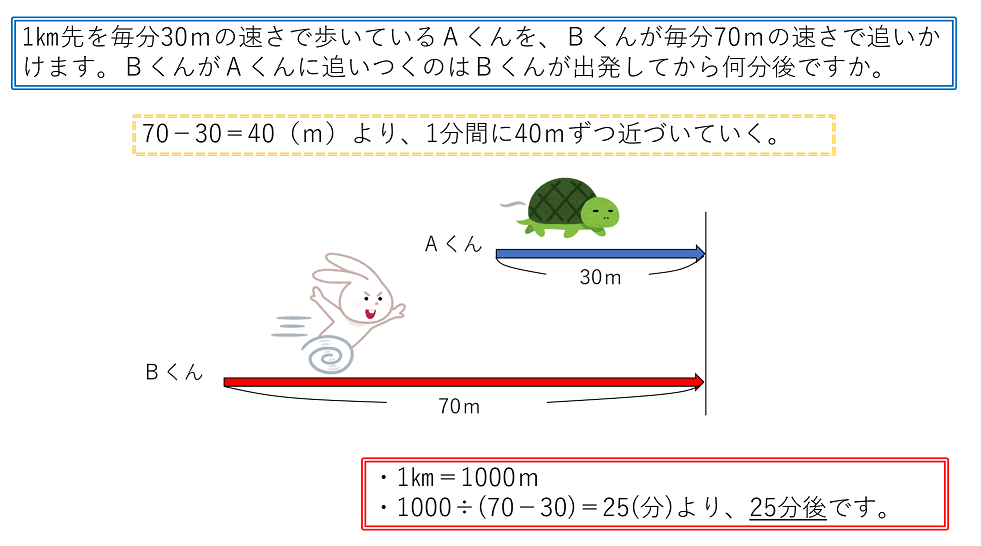
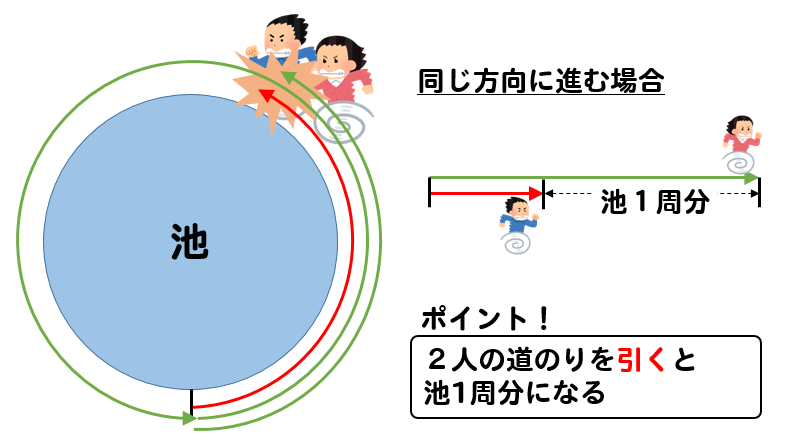
Mixi授業の工夫事典!!(塾講師・教師) 受験算数追いつくまでの時間と「速さの差」の比 お久しぶりです。 次のような速さの問題を質問されたのですが、その解法についての質問です。 「甲地点からA、Bが、乙地点からCが三人とも同じ向き（甲→乙→）に同時に出発した。そこからBくんが出発すると、速さの差から 2人の道のりの差は1分で40mずつ縮まる ことが分かります。 そして、この差が0になったときが追いついたときということになります。 よって、480mあった二人の差が1分間で40mずつ縮まっていくということを考えると旅人算（追いつく時間） 使いやすいです。 すごく楽だった。 旅人算で分からない問題が有ったからです?

旅人算 2人が追いつく問題の解き方は 数スタ

予習シリーズ第18 19回 旅人算 の予習 日々の学習 妹中学受験

はてブ LINE Pocket 今回は中2で学習する一次関数の単元から 一次関数の利用である「追いつく速さ」の問題を取り上げて解説していきます。 追いつく利用問題では、大きく分けて2パターンの出題があります。 ゴールまで一直線パターン 途中で休憩する分からなかった問題が解けました！ ありがとうございました！ すぐに計算できたので、大変便利で役に立ちました。 趣味です。 どれもこれも役

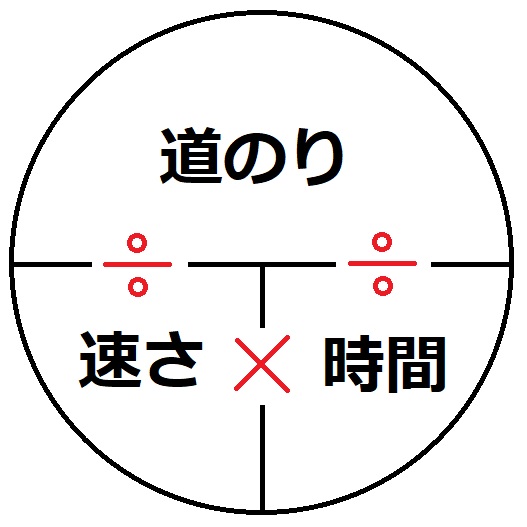
速さと時間から道のりを求める問題 家庭学習レシピ

旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学

方程式 速さの問題 追いつくのは何分後 解き方を解説 中学数学 理科の学習まとめサイト

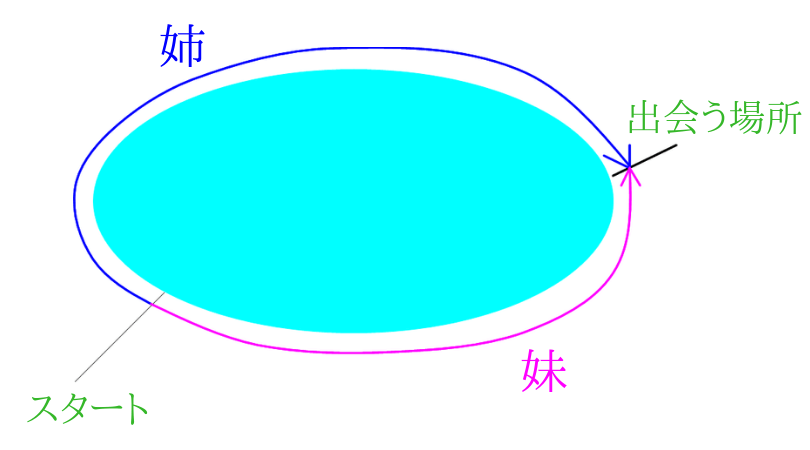
旅人算 池の周りで追いつく問題の解き方 考え方 算数パラダイス

旅人算 Wikipedia

中学受験 算数 速さの重点ポイントまとめ 比を使った裏技公開 中学受験アンサー

旅人算とグラフ 中学受験準備のための学習ドリル

中学数学 １次方程式 文章題の解き方 速さ 時間 道のり

例題あり 旅人算とは 出会い算 追いつき算など種類別の解き方や教え方のコツも解説 学びtimes

速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun

Vrで感じる算数 旅人算 小川俊介

1

中1 数学 中1 38 方程式の利用 ２つの速さ編 Youtube

数基礎 Com 追いつく旅人算が分かる方法

え こんなに簡単だったの 中学入試の分かりやすい旅人算の解き方 受験ボックス

文章題 速さ 追いつく1

旅人算の基本 図をかいて整理しよう

画像一覧 算数 数学が好きになりmath

え こんなに簡単だったの 中学入試の分かりやすい旅人算の解き方 受験ボックス

中学数学 １次方程式 文章題の解き方 速さ 時間 道のり

一次方程式 道のり 速さの文章問題 追いつく系 の解き方 Qikeru 学びを楽しくわかりやすく

小学５年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生

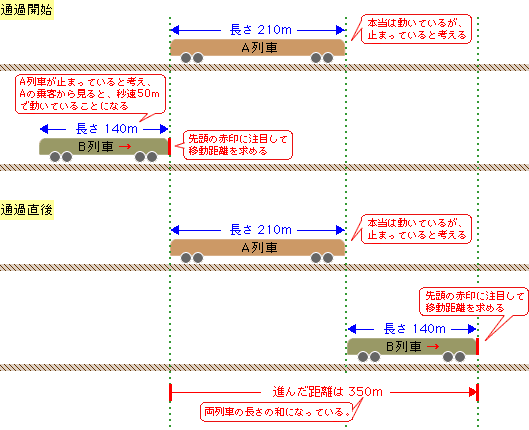
通過算 算数の教え上手 学びの場 Com

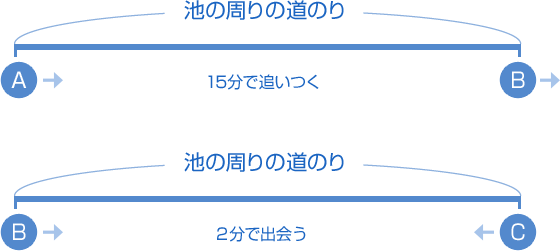
算数 速さと比 １ 中学受験 ベネッセ教育情報サイト

基本 旅人算の解き方 テクニック 中学受験 塾なし の勉強法

例題あり 旅人算とは 出会い算 追いつき算など種類別の解き方や教え方のコツも解説 学びtimes

一次方程式 道のり 速さの文章問題 追いつく系 の解き方 Qikeru 学びを楽しくわかりやすく

旅人算の苦手を克服 分かりやすく教える方法と解き方はコレ みけねこ小学校

中学受験 算数 速さの重点ポイントまとめ 比を使った裏技公開 中学受験アンサー

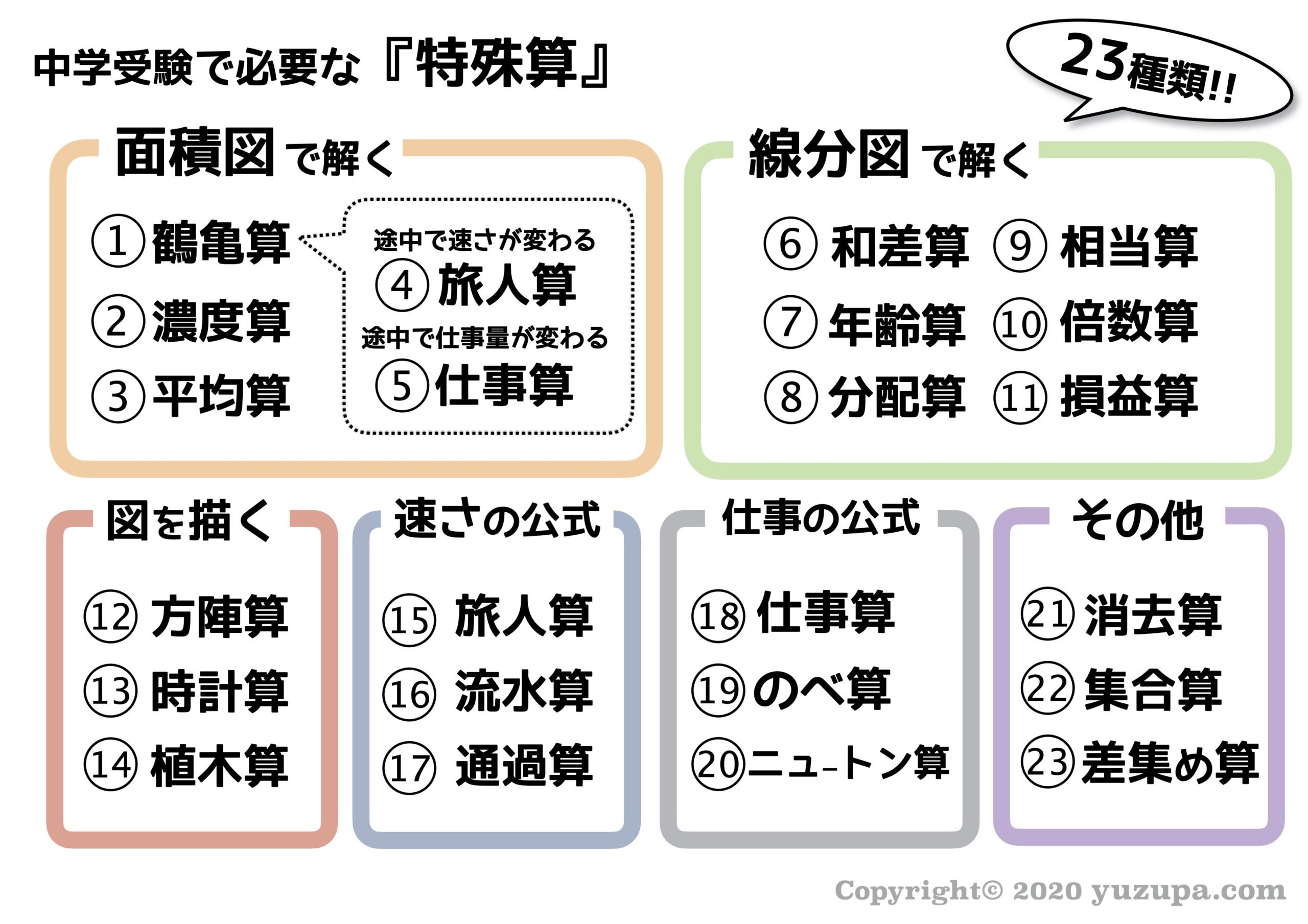
主な特殊算の公式 一覧 中学受験対策 Yattoke 小 中学生の学習サイト

中学受験算数 旅人算 の授業映像 プリント無料配布 Youtube スタディカフェ

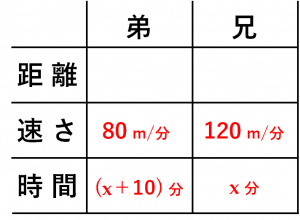
中1数学 方程式 方程式の利用 速さの文章題は表を使おう たけのこ塾 勉強が苦手な中学生のやる気をのばす

旅人算 算数の教え上手 学びの場 Com

ヤフオク ベイシック 基本６０題 算数 割合 比 速さ 中学

中1 数学 中1 37 方程式の利用 追いつく編 Youtube

旅人算

旅人算

小学6年生速さの問題が分かりません 今日教えないといけません み 数学 教えて Goo

小学6年生の算数の速さのまとめ みけねこ小学校

妹の宿題で 小学5年生の算数の問題なんですが 私も の式の立て方が分かりません 分か Clear

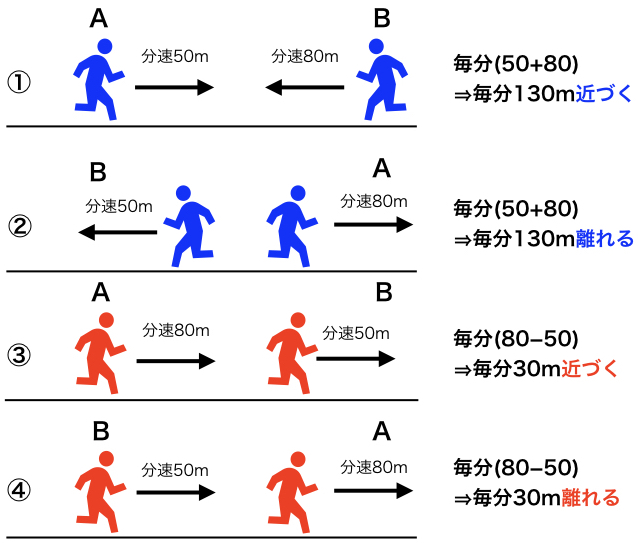
旅人算 わかりやすい出会い算と追いつき算の解き方を簡単計算 Landgather

算数文章題講座 旅人算の解き方 基本問題

算数文章題講座 旅人算の解き方 基本問題

小学６年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生

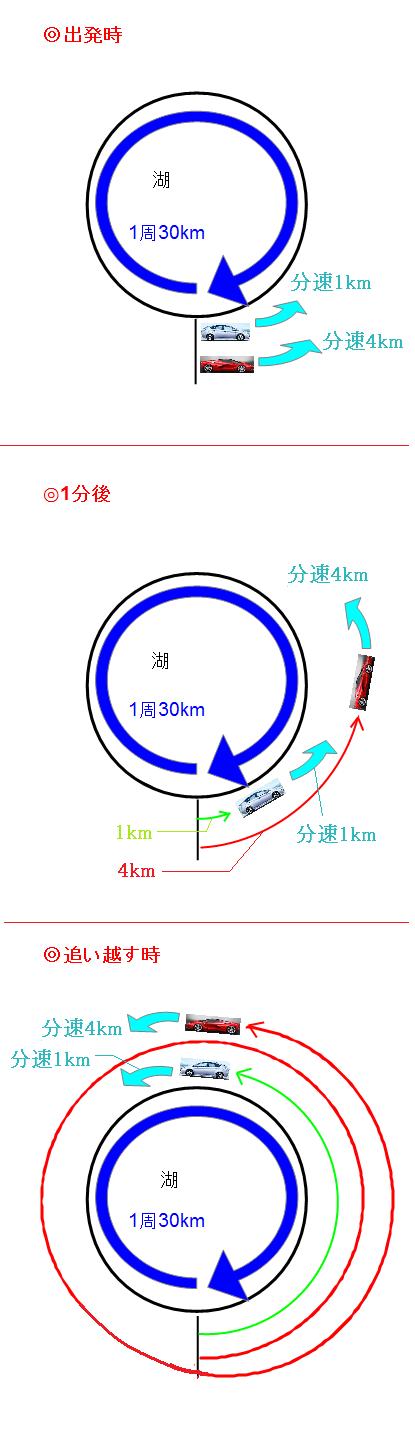
旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける

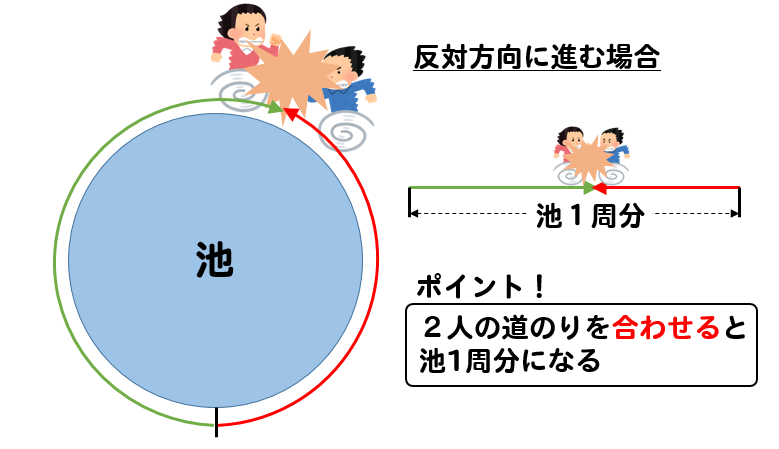
連立方程式 池の周りを追いつく速さの文章問題を解説 数スタ

速さ 中学受験ー算数解き方ポータル

方程式利用 何分後に追いつくか 速さの文章問題を徹底解説 数スタ

速さ 中学受験ー算数解き方ポータル

中学受験 特殊算は何種類ある 算数の文章題の見分け方 かるび勉強部屋

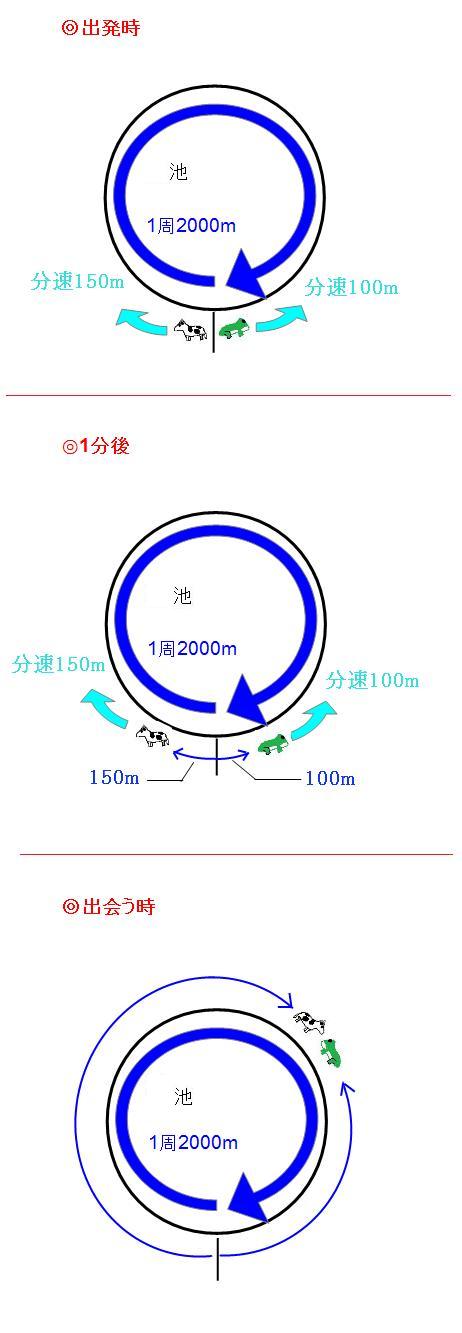
旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける

最高のコレクション 距離 時間 速さ 問題 ニスヌーピー 壁紙

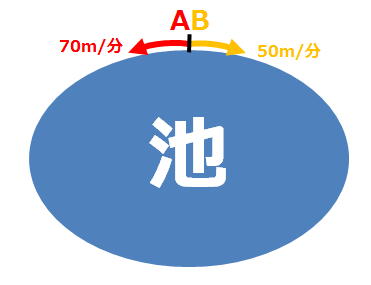
旅人算 池の周りを回る二人が出会う問題 の解き方

速さ みはじ や はじき で覚えていいの 旅人算攻略法 ふるやまんのマスラボ奮闘記

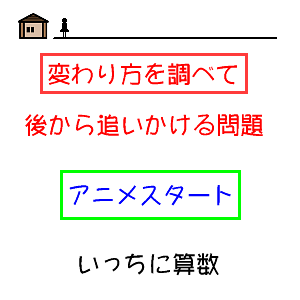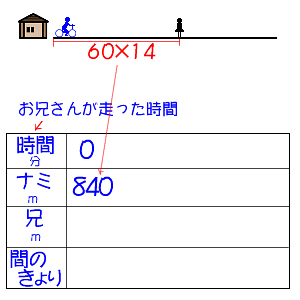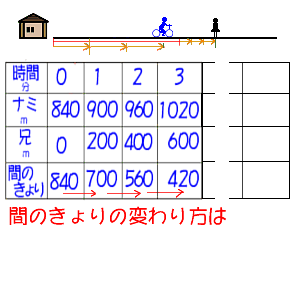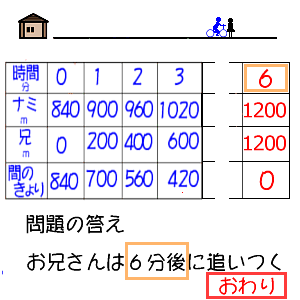
６年算数 変わり方を調べて １ 出会い算

旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける

中学受験 算数確認チェック25 速さ 速さの比 旅人算 グランパは元塾長

甲陽学院中２０１９年 旅人算ー 中学受験算数の良問 難問 基本問題

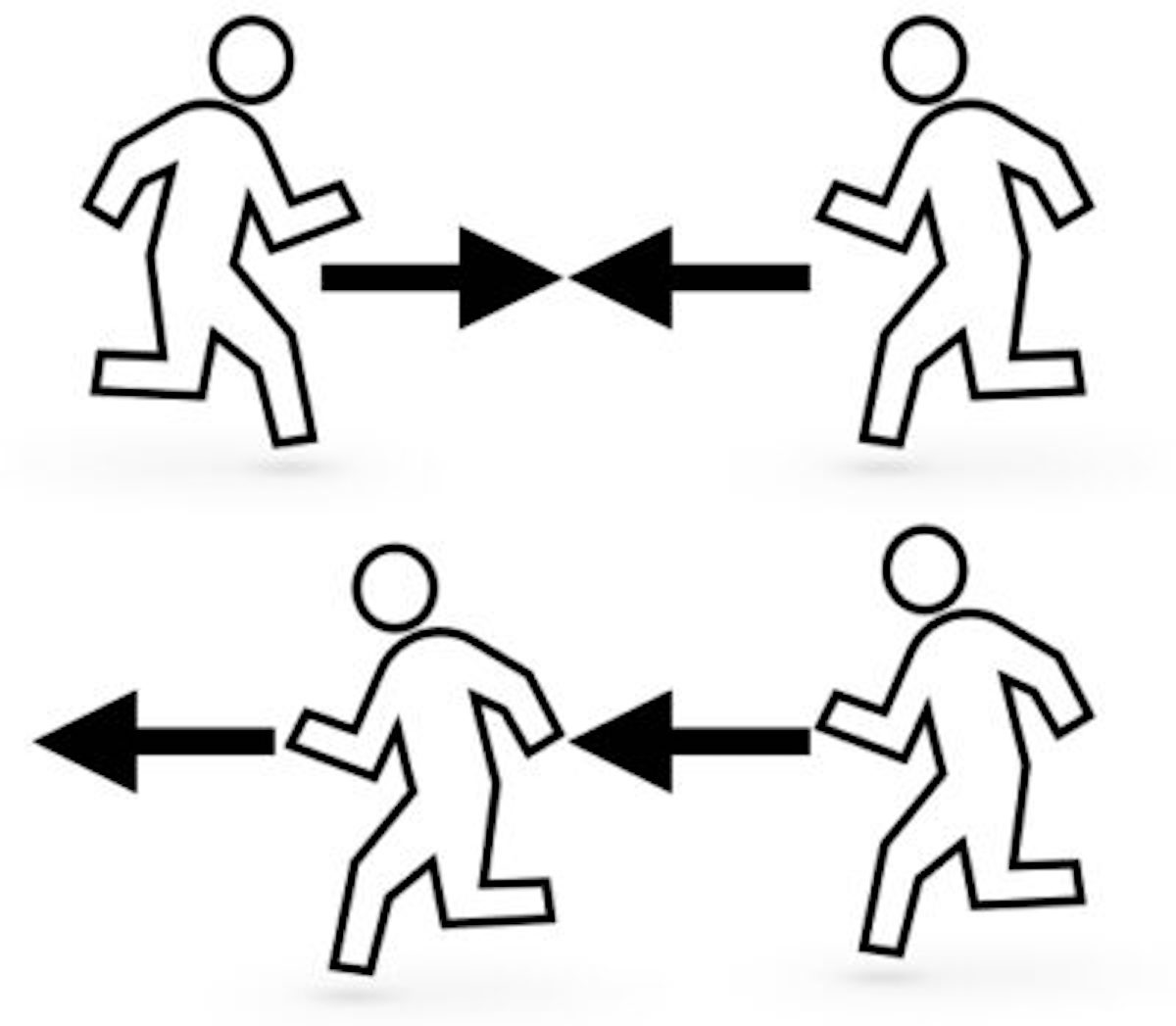
旅人算 わかりやすい出会い算と追いつき算の解き方を簡単計算 Landgather

算数文章題講座 旅人算の解き方 基本問題

速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun

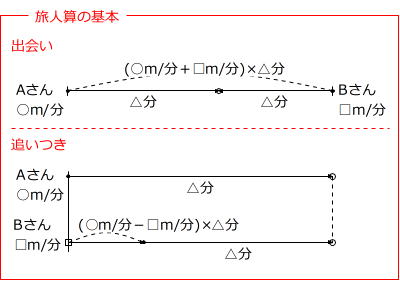
第492回 合否を分ける問題の解き方 旅人算 前田昌宏の中学受験が楽しくなる算数塾

旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun

旅人算の苦手を克服 分かりやすく教える方法と解き方はコレ みけねこ小学校

方程式 速さの問題 追いつくのは何分後 解き方を解説 中学数学 理科の学習まとめサイト

旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学

旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学

旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun

算数 速さ道のり 追いつき算 旅人算 Youtube

１次方程式 速さ 中学から数学だいすき

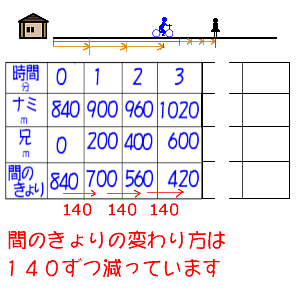
６年算数 変わり方を調べて １ 追いつき算

旅人算 2人が追いつく問題の解き方は 数スタ

慶應義塾普通部13年度算数入試問題5 旅人算 中学受験から医学部受験までプロにお任せ プロ家庭教師集団スペースone 公式

中学数学 １次方程式 文章題の解き方 速さ 時間 道のり

旅人算 算数の教え上手 学びの場 Com

連立方程式 池の周りを同じ方向 反対方向に回る問題を解説 Youtube

え こんなに簡単だったの 中学入試の分かりやすい旅人算の解き方 受験ボックス

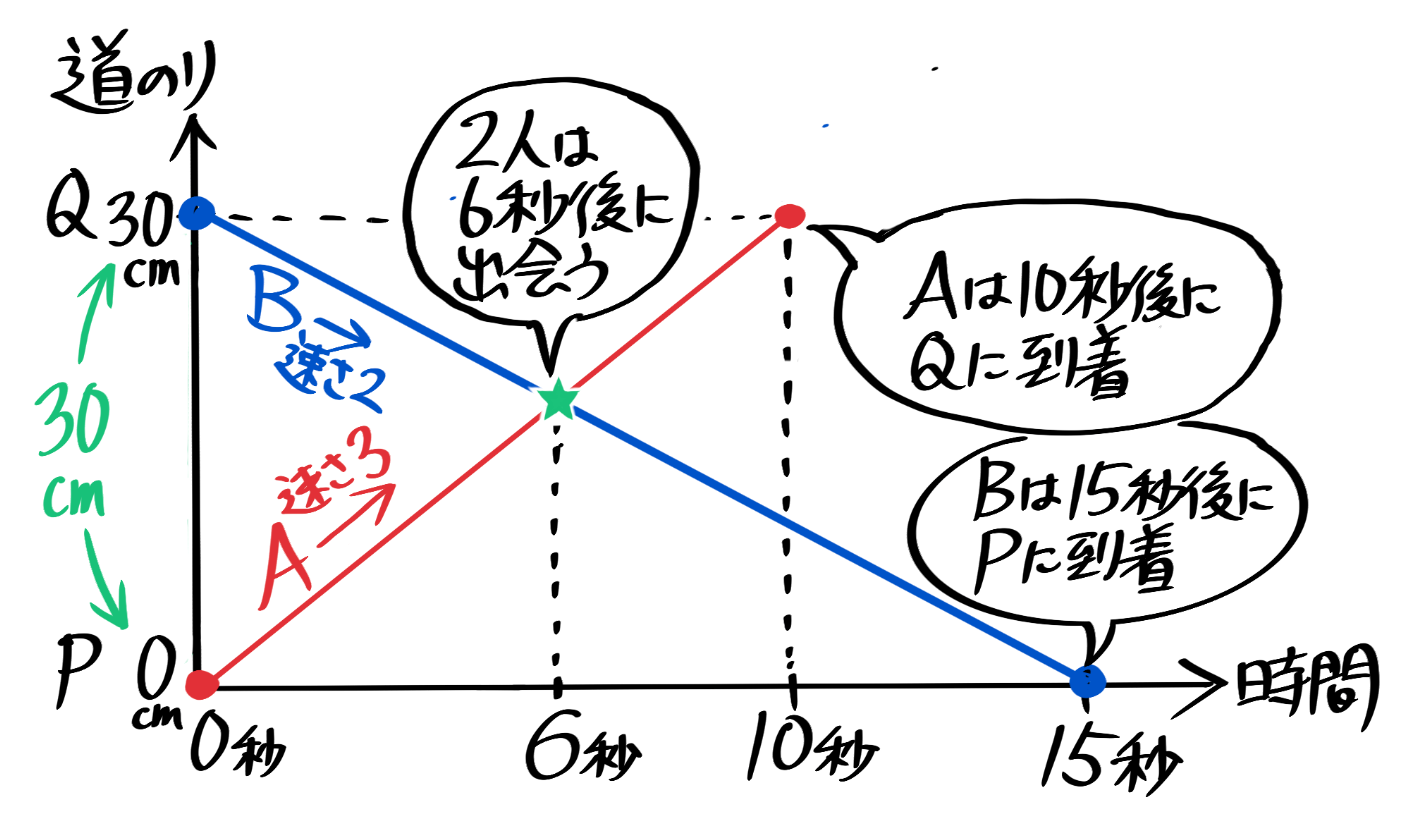
中学受験 旅人算とは 基本公式から往復など応用問題 ダイヤグラムまで そうちゃ式 受験算数 2号館 図形 速さ

1

中学受験算数 実力チェック 29速さと比 旅人 通過算 グランパは元塾長

3

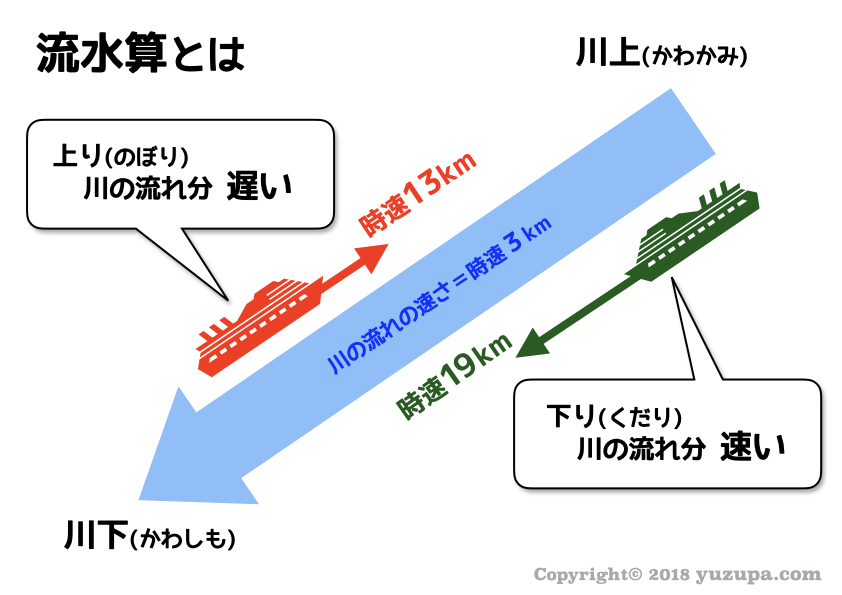
中学受験 流水算は ４つ速さを整理すれば簡単に解ける かるび勉強部屋

方程式 速さの問題 追いつくのは何分後 解き方を解説 中学数学 理科の学習まとめサイト

旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学

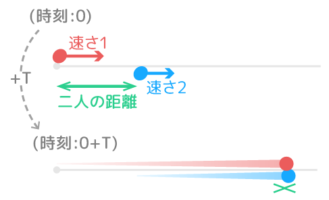
中学受験 旅人算とは 基本公式から往復など応用問題 ダイヤグラムまで そうちゃ式 受験算数 2号館 図形 速さ

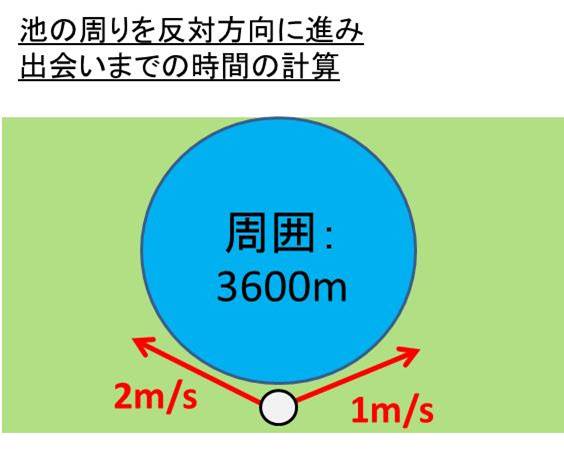
池の周りで出会う 追いつくなどの連立方程式の計算を行う方法 同じ方向 反対方向と速さ ウルトラフリーダム

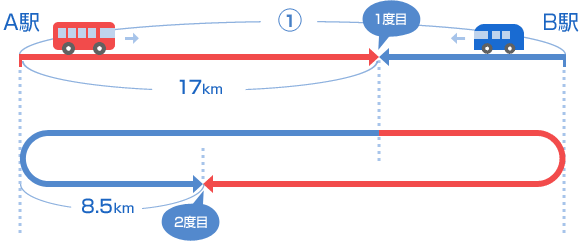
算数 速さ 旅人算 通過算 中学受験 ベネッセ教育情報サイト

５月９日 小６算数 ジャングルジムブログ

６年算数 変わり方を調べて １ 追いつき算

連立方程式 池の周りを追いつく速さの文章問題を解説 数スタ

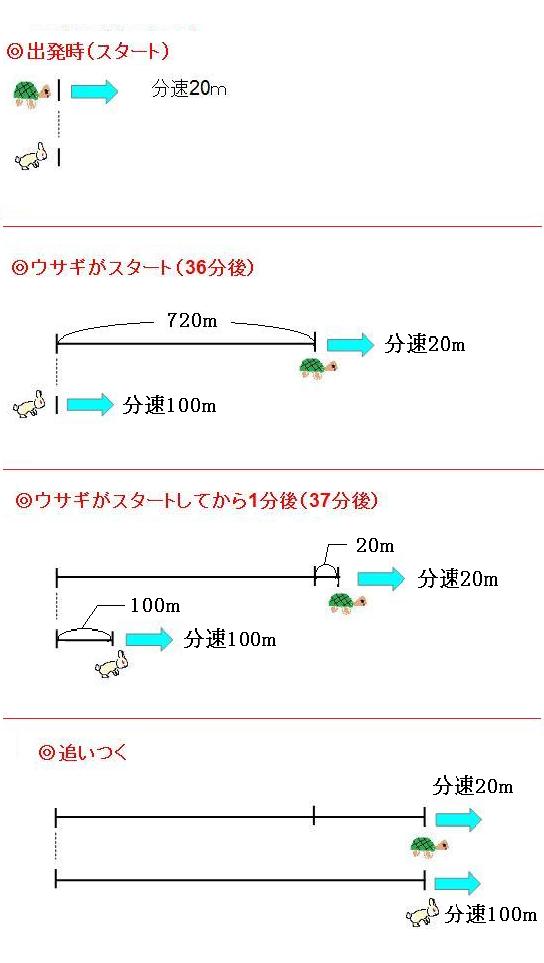
旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける

旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun

連立方程式 池の周りを追いつく速さの文章問題を解説 数スタ

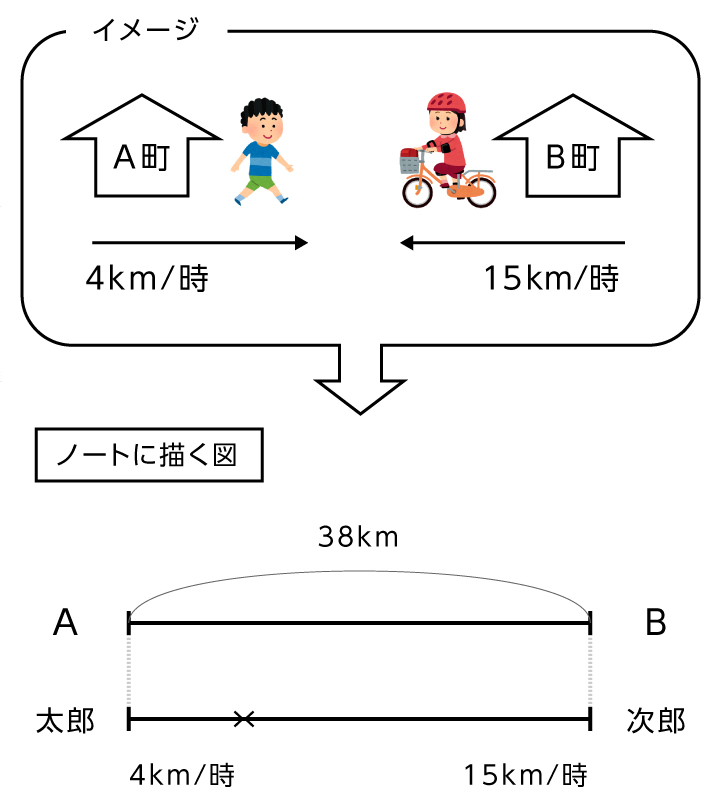
旅人算ってどんなもの 旅人算をわかりやすく解説 中学受験ナビ

Incoming Term: 算数 速さ 問題 追いつく,